已知 中,
中, ,D是
,D是 外接圆劣弧
外接圆劣弧 上的点(不与点A、C重合),延长BD至E.
上的点(不与点A、C重合),延长BD至E.
(1)求证:AD的延长线平分 CDE;
CDE;
(2)若 ,
, 中BC边上的高为2+
中BC边上的高为2+ ,求
,求 外接圆的面积.
外接圆的面积.
如图,三棱柱 中,
中, 平面
平面 ,
, ,
,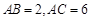 , 点
, 点 在线段
在线段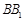 上,且
上,且 ,
, .
.
(Ⅰ)求证:直线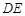 与平面
与平面 不平行;
不平行;
(Ⅱ)设平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为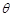 ,若
,若 ,求
,求 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面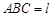 ,求直线
,求直线 与
与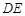 所成的角的余弦值.
所成的角的余弦值.
已知数列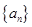 的前
的前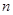 项和为
项和为 ,且
,且 .
.
(1)求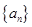 的通项公式;
的通项公式;
(2)设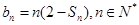 ,若
,若 恒成立,求实数
恒成立,求实数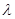 的取值范围;
的取值范围;
(3)设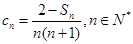 ,
,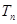 是数列
是数列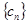 的前
的前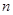 项和,证明
项和,证明 .
.
设函数 ,
,
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若 ,
, ,求
,求 的面积的最大值.
的面积的最大值.
已知函数 ,设
,设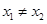 且
且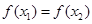 .
.
(1)证明: ,且
,且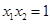 ;
;
(2)若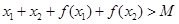 对任意满足条件的
对任意满足条件的 ,
,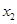 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
已知函数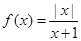 .
.
(1)求 的单调区间;
的单调区间;
(2)若方程 有四个不等实根,求实数
有四个不等实根,求实数 的取值范围.
的取值范围.