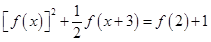如图,椭圆 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长.
的短轴长. 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 相交于点
相交于点 ,直线
,直线 分别与
分别与 相交于点
相交于点 .
.
(Ⅰ)求 、
、 的方程;
的方程;
(Ⅱ)求证: ;
;
(Ⅲ)记 的面积分别为
的面积分别为 ,若
,若 ,求
,求 的取值范围
的取值范围
已知向量m=(sinA,cosA),n=(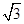 ,-1),m·n=1,且A为锐角.
,-1),m·n=1,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
| y(米) |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
1.0 |
0.5 |
0.99 |
1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多长时间可供冲浪者进行运动?
平面直角坐标系xOy内有向量 =(1,7),
=(1,7),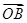 =(5,1),
=(5,1), =(2,1),点Q为直线OP上一动点.
=(2,1),点Q为直线OP上一动点.
(1)当 ·
·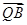 取得最小值时,求
取得最小值时,求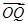 坐标;
坐标;
(2)当点Q满足(1)中条件时,求cos∠AQB的值.
(1)已知α是第一象限的角,且cosα=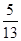 ,求
,求 的值.
的值.
(2)化简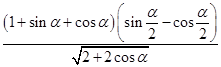 ,其中π<α<2π.
,其中π<α<2π.
设定义在 上的函数
上的函数 ,满足当
,满足当 时,
时, ,且对任意
,且对任意 ,有
,有 ,
,
(1)解不等式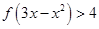
(2)解方程