若某产品的直径长与标准值的差的绝对值不超过
时，则视为合格品，否则视为不合格品．在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品．计算这50件不合格品的直径长与标准值的差（单位：
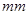）将所得数据分组，得到如下频率分布表：
（1）将上面表格中缺少的数据填充完整；
（2）估计该厂生产的此种产品中，不合格的直径长与标准值的差落在区间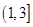
内的概率
（3）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品，据此估算这批产品中的合格品的件数．
已知某几何体的俯视图是如图所示的矩形，正视图（或称主视图）是一个底边长为8、高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为4的等腰三角形．
（1）求该几何体的体积V；
（2）求该几何体的侧面积S
（本小题满分12分）设圆满足：①截
轴所得弦长为2；②被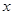
轴分成两段圆弧,其弧长的比为
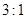；在满足条件①和②的所有圆中,求圆心到直线
的距离最小的圆的方程．
（本小题满分12分）已知M为圆C：x2＋y2－4x－14y＋45＝0上任意一点，且点Q（－2,3）．
（1）求|MQ|的最大值和最小值；
（2）若M（m，n），求
的最大值和最小值
（本小题满分12分）已知点
到直线l：
的距离为
．数列{an}的首项
，且点列
均在直线l上．
（Ⅰ）求b的值；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）求数列
的前n项和
．
（本小题满分12分） 某投资公司计划投资A，B两种金融产品，根据市场调查与预测，A产品的利润y1与投资金额x的函数关系为y1＝18－
，B产品的利润y2与投资金额x的函数关系为y2＝
，（注：利润与投资金额单位：万元）
（1）该公司已有100万元资金，并全部投入A，B两种产品中，其中x万元资金投入A产品，
试把A，B两种产品利润总和表示为x的函数，并写出定义域；
（2）在（1）的条件下，怎样分配这100万元资金，才能使公司获得最大利润？其最大利润为多少万元？