已知△ABC的三个顶点 ,其外接圆为圆H.
,其外接圆为圆H.
(1)求圆H的方程;
(2)若直线l过点C,且被圆H截得的弦长为2,求直线l的方程;
(3)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M、N,使得点M是线段PN的中点,求圆C的半径r的取值范围.
(本小题满分12分)
已知圆C的圆心为原点O,且与直线x+y+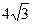 =0相切.
=0相切.
(1)求圆C的方程;
(2)点P在直线x=8上,过P点引圆C的两条切线PA、PB,切点为A、B,求证:直线AB恒过定点.
设 ,在线段
,在线段 上任取两点C,D(端点
上任取两点C,D(端点 除外),将线段
除外),将线段 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| 1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
| X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 6 |
0.05 |
0.32 |
0.38 |
0.73 |
| Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0 .86 .86 |
| 11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
| X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 64 |
0.36 |
0.35 |
0.95 |
0.14 |
| Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是 之间的均匀随机
之间的均匀随机 数)
数)
(本小题满分12分)
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
(本小题满分12分)
现有8名奥运会志愿者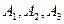 通晓日语,
通晓日语,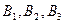 通晓俄语,
通晓俄语, 通晓韩语。从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语。从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求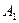 被选中的概率
被选中的概率 ;(2)求
;(2)求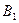 和
和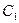 不全被选中的概率.
不全被选中的概率.
(本小题满分12分)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如下: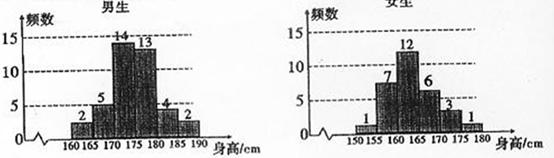
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.