小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该年每年的运输收入均为25万元,小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第 年年底出售,其销售价格为
年年底出售,其销售价格为 万元(国家规定大货车的报废年限为10年).
万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=运输累计收入+销售收入-总支出)
已知双曲线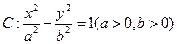 的离心率为
的离心率为 ,右准线方程为
,右准线方程为 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆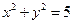 上,求m的值.
上,求m的值.
(本小题满分12分)
设数列 的前
的前 项和为
项和为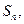 已知
已知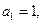
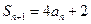
(I)设 ,证明数列
,证明数列 是等比数列;
是等比数列;
(II)求数列 的通项公式。
的通项公式。
(本小题满分12分)
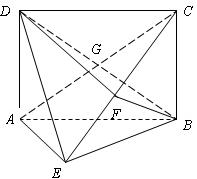
如图,矩形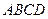 中,
中,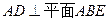 ,
,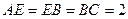 ,
,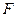 为
为 上的点,且
上的点,且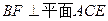 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证;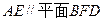 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(本小题共12)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
(本小题满分10分)
在△ 中,
中, 所对的边分别为
所对的边分别为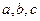 ,
, ,
, .
.
(1)求 ;
;
(2)若 ,求
,求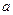 ,
, ,
,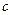 .
.