我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;
谷时(晚21:00~早8:00)0.36元/度.
已知小明家下月计划总用电量为400度,
(1)若其中峰时电量为100度,则小明家按照哪种方式付电费比较合适?能省多少元?
(2)峰时电量为多少度时,两种方式所付的电费相等?
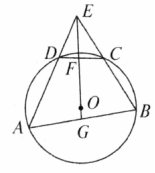
如图,已知 是四边形 的外接圆,直线 相交于点 是弦 的中点,延长直线 交弦 于点 ,求证:
(1) ;
(2) .
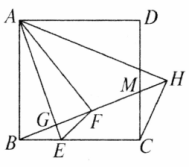
如图,已知正方形 ,点 是 边上一点,将 沿直线 折叠,点 落在 处,连接 并延长,与 的平分线相交于点 ,与 分别相交于点 , ,连接 .
(1)求证:
(2)若 ,求点 到直线 的距离;
(3)当点 在 边上(端点除外)运动时, 的大小是否变化?为什么?
如图所示,在 中, 为 边上一点, 是方程 的一个较大的根,求 的长

如图,已知 中, 是 的外接圆, 是 边上的高, 是 的垂心,连接 ,连接 并延长交 于点 ,交 于点 ,求证:
(1) ;
(2) 等于 外接圆半径;
(3) .

如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 两点.
(1)求抛物线的解析式;
(2)如图,点 是直线 上方抛物线上的一动点,当 面积最大时,请求出点 的坐标和 面积的最大值?
