观察下图,每个小正方形的边长均为1,可以得到每个小正方形的面积为1.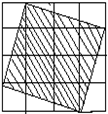
(1)图中阴影部分的面积是多少? 阴影部分正方形的边长是多少?
(2)估计边长的值在哪两个整数之间?
(3)请你利用图形在数轴上用刻度尺和圆规表示阴影部分正方形边长所表示的数。
计算: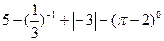
对非负实数x“四舍五入”到个位的值记为
即:当n为非负整数时,如果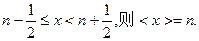
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:① =(
=(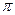 为圆周率);
为圆周率);
②如果 的取值范围为;
的取值范围为;
(2)①当 ;
;
②举例说明 不恒成立;
不恒成立;
(3)求满足 的值;
的值;
(4)设n为常数,且为正整数,函数 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为 的个数记为b.
的个数记为b.
求证: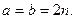
如图,在直角坐标系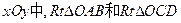 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
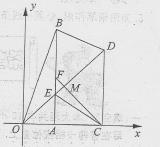
试解决下列问题:
(1)填空:点D坐标为;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD= ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为.
海宝在研究数学问题时发现了一个有趣的现象:
(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.