某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| f |
a |
0.2 |
0.45 |
b |
c |
(Ⅰ)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,
他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望. 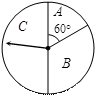
已知函数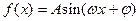
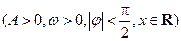 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数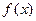 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.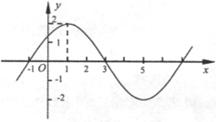
(本小题满分14分)
设函数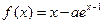 。
。
(I)求函数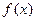 单调区间;
单调区间;
(II)若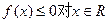 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(III)对任意n的个正整数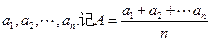
(1)求证: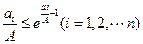 (2)求证:
(2)求证: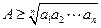
(本小题满分13分)
在数列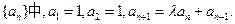
(I)若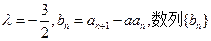 是公比为β的等比数列,求α和β的值。
是公比为β的等比数列,求α和β的值。
(II)若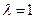 ,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得
,基于事实:如果d是a和b的公约数,那么d一定是a-b的约数。研讨是否存在正整数k和n,使得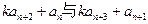 有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
有大于1的公约数,如果存在求出k和n,如果不存在请说明理由。
(本小题满分12分)
已知点 是椭圆
是椭圆 上任意一点
上任意一点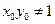 ,直线
,直线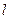 的方程为
的方程为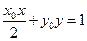
(I)判断直线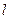 与椭圆E交点的个数;
与椭圆E交点的个数;
(II)直线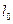 过P点与直线
过P点与直线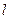 垂直,点M(-1,0)关于直线
垂直,点M(-1,0)关于直线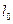 的对称点为N,直线PN恒
的对称点为N,直线PN恒
过一定点G,求点G的坐标。