某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
设函数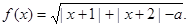
(1)当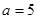 时,求函数
时,求函数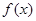 的定义域;
的定义域;
(2)若函数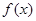 的定义域为R,试求
的定义域为R,试求 的取值范围。
的取值范围。
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线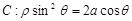
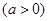 ,过点
,过点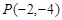 的直线
的直线 的参数方程为:
的参数方程为:
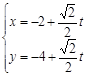 ,(t为参数),直线
,(t为参数),直线 与曲线
与曲线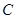 分别交于
分别交于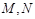 两点.
两点.
(1)写出曲线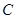 和直线
和直线 的普通方程;
的普通方程;
(2)若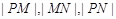 成等比数列,求
成等比数列,求 的值.
的值.
如图,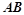 是⊙
是⊙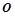 的一条切线,切点为
的一条切线,切点为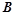 ,
, 都是⊙
都是⊙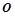 的割线,已知
的割线,已知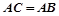 .
.
(1)证明: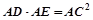 ;
;
(2)证明: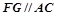 .
.
已知f(x)=xlnx.
(I)求f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)证明: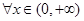 都有
都有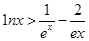 。
。
某厂生产产品x件的总成本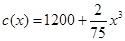 (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?