把一颗骰子投掷2次，观察出现的点数，并记第一次出现的点数为a，第二次出现的点数为b，试就方程组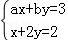
解答下列各题：
（1）求方程组只有一个解的概率；
（2）求方程组只有正数解的概率．
（本小题满分12分）
已知函数
，其中
为正实数。
（1）当
时，求
在
上的零点个数。
（2）对于定义域内的任意
，将
的最大值记作
，求的表达式。
（本小题满分12分）
已知椭圆
的中心在坐标原点，焦点在
轴上，离心率为
，它的一个焦点恰好是抛物线
的焦点。
（1）求椭圆的方程；
（2）设
为椭圆的一条不垂直于轴的弦，且过点
。过
作关于的对称点
，证明：直线
过轴的一个定点。
（本小题满分12分）
网上购物逐步走进大学生活，某大学学生宿舍4人积极参加网购，大家约定：每个人通过掷一枚质地均匀的骰子决定自己去哪家购物，掷出点数为5或6的人去淘宝网购物，掷出点数小于5的人去京东商城购物，且参加者必须从淘宝网和京东商城选择一家购物。
（1）求这4个人中恰有1人去淘宝网购物的概率；
（2）用
分别表示这4个人中去淘宝网和京东商城购物的人数，集
，求随机变量
的分布列与数学期望
。
（本小题满分12分）
如图，在三棱锥
中，
平面
，
为
的中点，
分别为线段
上的动点，且
。
（1）求证：
面
；
（2）若
是
的中点，
是线段
靠近
的一个三等分点，求二面角
的余弦值。
（本小题满分12分）
已知函数
。
（1）求
的最小正周期
（2）若将的图像向右平移
个单位，得到函数
的图像，求函数的单调递增区间。