(本小题满分12分)
如图,在三棱锥 中,
中, 平面
平面 ,
, 为
为 的中点,
的中点, 分别为线段
分别为线段 上的动点,且
上的动点,且 。
。
(1)求证: 面
面 ;
;
(2)若 是
是 的中点,
的中点, 是线段
是线段 靠近
靠近 的一个三等分点,求二面角
的一个三等分点,求二面角 的余弦值。
的余弦值。
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
(1)求证:平面ABM 平面PCD;
平面PCD;
(2)求三棱锥M-ABD的体积.
某学校准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175以下(不包括175cm)定义为“不合格”
(1)求甲队队员跳高成绩的中位数
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人,则5人中“合格”与“不合格”的人数各为多少?
(3)从甲队178cm以上(包括178cm)选取2人,至少有一人在186cm以上(包括186cm)的概率为多少?
如图1,在直角梯形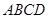 中,
中,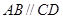 ,
,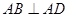 ,且
,且 .现以
.现以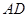 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边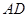 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面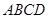 垂直,
垂直,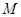 为
为 的中点,如图2.
的中点,如图2.
(1)求证: ∥平面
∥平面 ;
;
(2)求证: 平面
平面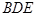 ;
;
(3)求点 到平面
到平面 的距离.
的距离.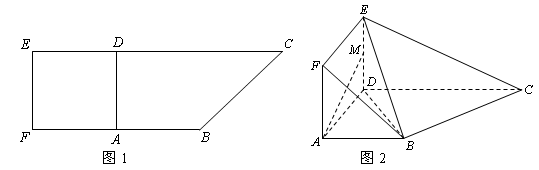
已知圆的极坐标方程为: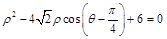 .
.
(1)将极坐标方程化为普通方程;
(2)若点 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.
已知函数
(1)试判断函数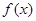 的单调性;
的单调性;
(2)设 ,求
,求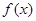 在
在 上的最大值;
上的最大值;
(3)试证明:对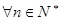 ,不等式
,不等式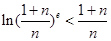 .
.