已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(Ⅰ)若 =
=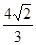 ,求
,求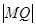 及直线MQ的方程;
及直线MQ的方程;
(Ⅱ)求证:直线AB恒过定点.
(Ⅰ)已知正数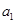 、
、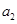 满足
满足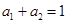 ,求证:
,求证: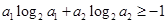 ;
;
(Ⅱ)若正数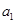 、
、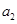 、
、 、
、 满足
满足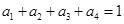 ,
,
求证: .
.
已知定点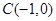 及椭圆
及椭圆 ,过点
,过点 的动直线与该椭圆相交于
的动直线与该椭圆相交于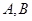 两点.
两点.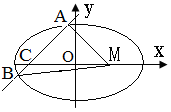
(Ⅰ)若线段 中点的横坐标是
中点的横坐标是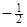 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)在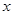 轴上是否存在点
轴上是否存在点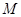 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点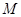 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2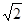 ,SA=SB=
,SA=SB= .
.
(Ⅰ)求证:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的正弦值.
已知数列{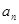 }中,
}中, 为其前n项和,且
为其前n项和,且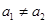 ,当
,当 时,恒有
时,恒有 (
( 为常数).
为常数).
(Ⅰ)求常数 的值;
的值;
(Ⅱ)当 时,求数列{
时,求数列{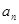 }的通项公式;
}的通项公式;
(Ⅲ)设 ,数列
,数列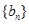 的前n项和为
的前n项和为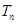 ,求证:
,求证: .
.
从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.
(Ⅰ)求从该批产品中任取1件是二等品的概率 ;
;
(Ⅱ)若该批产品共20件,从中任意抽取2件,X表示取出的2件产品中二等品的件数,求X的分布列与期望.