已知数列{an}的前n项和为Sn,且a1= .
.
(1)求{an}的通项公式;
(2)设bn=n(2﹣Sn),n∈N*,若bn≤λ,n∈N*恒成立,求实数λ的取值范围.
(3)设Cn= ,Tn是数列{Cn}的前n项和,证明
,Tn是数列{Cn}的前n项和,证明 ≤Tn<1.
≤Tn<1.
给定椭圆 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是 .
.
(1)若椭圆C上一动点 满足
满足 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为 ,求P点的坐标;
,求P点的坐标;
(3)已知 ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点 的直线的最短距离
的直线的最短距离 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
某种海洋生物身体的长度 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值.
已知函数 .
.
(1)若 ,求实数x的取值范围;
,求实数x的取值范围;
(2)求 的最大值.
的最大值.
在△ABC中,BC=a,AC=b,a、b是方程 的两个根,且
的两个根,且 ,求△ABC的面积及AB的长.
,求△ABC的面积及AB的长.
已知函数 过点
过点 .
.
(1)求实数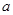 ;
;
(2)将函数 的图像向下平移1个单位,再向右平移
的图像向下平移1个单位,再向右平移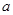 个单位后得到函数
个单位后得到函数 图像,设函数
图像,设函数 关于
关于 轴对称的函数为
轴对称的函数为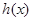 ,试求
,试求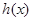 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.