已知椭圆 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点(
,且过点( ,
, ).
).
(1)求椭圆方程;
(2)设不过原点O的直线l:y=kx+m(k≠0),与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为k1、k2,满足4k=k1+k2,试问:当k变化时,m2是否为定值?若是,求出此定值,并证明你的结论;若不是,请说明理由.
叙述并证明余弦定理
(本小题满分14分)数列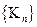 定义如下:
定义如下: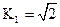 ,
,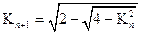 ,
,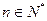 .
.
(1)求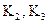 的值;
的值;
(2)求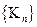 的通项;
的通项;
(3)若数列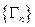 定义为:
定义为: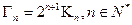 ,
,
①证明: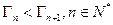 ;②证明:
;②证明: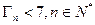 .
.
(本小题满分14分)已知函数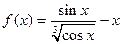
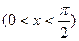 .
.
(1)求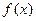 的导数
的导数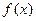 ;
;
(2)求证:不等式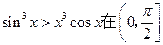 上恒成立;
上恒成立;
(3)求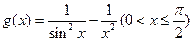 的最大值.
的最大值.
(本小题满分13分)已知抛物线C: 与直线l:
与直线l: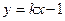 没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
(1)证明:直线AB恒过定点Q;
(2)若点P与(1)中的定点Q的连线交抛物线C于M,N两点,证明: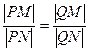 .
.
如图,已知斜三棱柱 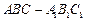 的底面是直角三角形,
的底面是直角三角形,  ,侧棱与底面所成的角为
,侧棱与底面所成的角为  ,点
,点  在底面上的射影
在底面上的射影  落在
落在  上.
上. 
(1)若点  恰为
恰为  的中点,且
的中点,且  ,求
,求 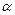 的值.
的值.
(2)若  ,且当
,且当 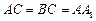 时,求二面角
时,求二面角 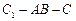 的大小.
的大小.