已知圆C: 内有一点P
内有一点P ,过点P作直线
,过点P作直线 交圆C与A,B两点
交圆C与A,B两点
(1)当 经过圆心C时,求直线
经过圆心C时,求直线 方程
方程
(2)当弦AB被点P平分时,求直线 方程
方程
(3)求过点(4,3)且与圆相切的直线方程
(本小题满分10分)设函数 (其中
(其中 >
>
0, ),且
),且 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求 的最小正周期;
的最小正周期;
(2)如果 在区间
在区间 上的最小值为
上的最小值为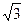 ,求a的值.
,求a的值.
(本小题满分10分)已知
 =
= ,
, =
= ,
,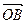 =
= ,设
,设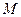 是直
是直
线 上一点,
上一点, 是坐标原点
是坐标原点
⑴求使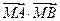 取最小值时的
取最小值时的 ;
; 
⑵对(1)中的点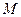 ,求
,求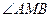 的余弦值。
的余弦值。
(本小题满分8分)已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、
黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)列出一次任取2个球的所有基本事件;
(3)从中取2个球,求至少有一个红球的概率.
(本小题满分8分)已知角 的终边在
的终边在 上,求
上,求
(1) 的值;
的值;
(2)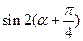 的值.
的值.