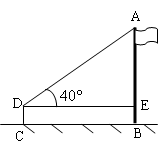
如图所示,课外活动中,小明在离旗杆AB的10米C处,用测角仪测得旗杆顶部A的仰角 ,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:
,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据: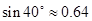 ,
,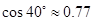 ,
,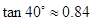 )
)
画出数轴,在数轴上表示下列各数: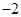 ,1.5,0,
,1.5,0, ,4,并回答问题:
,4,并回答问题:
(1)按从小到大的顺序用“<”连接上面各数;
(2)在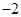 ,1.5,0,
,1.5,0, ,4这五个数中,任取二个数相乘,其中最大的积是 *.
,4这五个数中,任取二个数相乘,其中最大的积是 *.
我们知道,平方差公式是: (a+b)(a-b) = a2 - b2,反过来得到:a2 - b2=(a+b)(a-b)也成立,在解决某些问题时逆用平方差公式会起到很好的效果,如:计算:
根据平方差逆用方法,请计算下列各题:
(1)  ;(2分)
;(2分)
(2) 正整数m、n满足m2- n2=7,求m、n的值.(3分)
如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠3的度数.
有一张明星演唱会的门票,小明和小亮都想获得这张门票,亲自体验明星演唱会的热烈气氛,小红为他们出了一个主意,方法就是:从印有1、2、3、4、5、4、6、7的8张扑克牌中任取一张,抽到比4大的牌,小明去;否则,小亮去.
(1)求小明抽到4的概率;
(2)你认为这种方法对小明和小亮公平吗?请说明理由;若不公平,请你修改游戏规则,使游戏对双方都公平.
已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:EF∥CD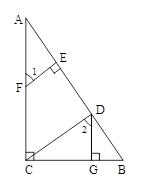
证明:∵ DG⊥BC,AC⊥BC( )
∴ ∠DGB=∠ACB=90º(垂直的定义)
∴ DG∥AC ( )
∴ ∠2 = ( )
∵ ∠1=∠2 ( )
∴ ∠1=∠DCA(等量代换)
∴ EF∥CD ( )