选修4-4:坐标系与参数方程选讲
已知在直角坐标系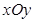 中,直线
中,直线 的参数方程为
的参数方程为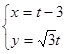 ,(
,( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线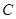 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求直线 的普通方程和曲线
的普通方程和曲线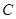 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点 是曲线
是曲线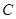 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离
的距离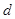 的取值范围.
的取值范围.
设数列 满足
满足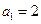 ,
,
(Ⅰ)求数列 的通项公式:
的通项公式:
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分10分)选修4—5;不等式选讲
设函数f(x)=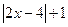
(Ⅰ)画出函数y=f(x)的图像;
(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.
(本小题满分10分)选修4—4;坐标系与参数方程
已知直线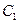 :
: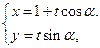 (t为参数),圆
(t为参数),圆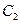 :
: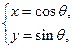 (
(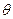 为参数),
为参数),
(Ⅰ)当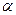 =
=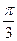 时,求
时,求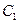 与
与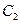 的交点坐标;
的交点坐标;
(Ⅱ)过坐标原点O作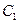 的垂线,垂足为A,P为OA的中点,当
的垂线,垂足为A,P为OA的中点,当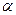 变化时,求P点轨迹的参数方程,并指出它是什么曲线;
变化时,求P点轨迹的参数方程,并指出它是什么曲线;
已知抛物线C的顶点在原点, 焦点为F(0, 1).
(Ⅰ) 求抛物线C的方程;
(Ⅱ)在抛物线C上是否存在点P, 使得过点P
的直线交C于另一点Q, 满足PF⊥QF, 且
PQ与C在点P处的切线垂直?
若存在, 求出点P的坐标; 若不存在,请说明理由.
(本题15分)已知函数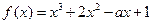 .
.
(I)若函数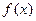 在点
在点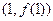 处的切线斜率为4,求实数
处的切线斜率为4,求实数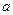 的值;
的值;
(II)若函数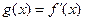 在区间
在区间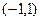 上存在零点,求实数
上存在零点,求实数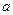 的取值。
的取值。