.(本小题满分13分)
已知椭圆 的焦点为
的焦点为 ,
,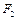 ,
,
离心率为 ,直线
,直线 与
与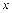 轴,
轴,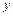 轴分别交于点
轴分别交于点 ,
, .
.
(Ⅰ)若点 是椭圆
是椭圆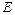 的一个顶点,求椭圆
的一个顶点,求椭圆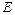 的方程;
的方程;
(Ⅱ)若线段 上存在点
上存在点 满足
满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)
如图,矩形 所在的平面与平面
所在的平面与平面 垂直,且
垂直,且 ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ) 求证:直线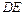 与平面
与平面 平行;
平行;
(Ⅱ)若点 在直线
在直线 上,且二面角
上,且二面角 的大小为
的大小为 ,试确定点
,试确定点 的位置.
的位置.
(本小题 满分13分)
满分13分)
已知函数 在
在 处取得最值.
处取得最值.
(Ⅰ)求函数 的最小正周期及
的最小正周期及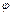 的值;
的值;
(Ⅱ)若数列 是首项与公差均为
是首项与公差均为 的等差数列,求
的等差数列,求 的值.
的值.
4-5(不等试证明)
已知
(Ⅰ)若 的取值范围;
的取值范围;
(Ⅱ)若不等式 的解集为R,求实数
的解集为R,求实数 的取值范围。
的取值范围。
((本小题满分10分)4-4(坐标系与参数方程)
已知曲线 与直线
与直线 为参数)相切,求实数
为参数)相切,求实数 的值。
的值。