选修4-1:几何证明选讲
如图,直线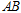 经过
经过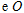 上的点
上的点 ,并且
,并且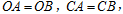
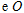 交直线
交直线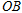 于
于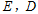 ,连结
,连结
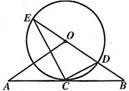
(Ⅰ)证明:直线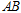 是
是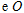 的切线;
的切线;
(Ⅱ)若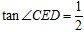 ,
,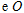 的半径为3,求
的半径为3,求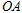 的长.
的长.
已知函数 ,斜率为
,斜率为 的直线与
的直线与 相切于
相切于 点.
点.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)当实数 时,讨论
时,讨论 的极值点。
的极值点。
(Ⅲ)证明: .
.
设 分别为椭圆
分别为椭圆 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于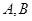 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
,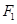 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的焦距;
的焦距;
(2)如果 ,求椭圆
,求椭圆 的方程
的方程
某唱片公司要发行一张名为《春风再美也比不上你的笑》的唱片,包含《新花好月圆》、《荷塘月色》等10首创新经典歌曲。该公司计划用 (百万元)请李子恒老师进行创作,经调研知:该唱片的总利润
(百万元)请李子恒老师进行创作,经调研知:该唱片的总利润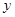 (百万元)与
(百万元)与 成正比的关系,当
成正比的关系,当 时
时 .又有
.又有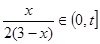 ,其中
,其中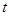 是常数,且
是常数,且 .
.
(Ⅰ)设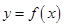 ,求其表达式,定义域(用
,求其表达式,定义域(用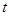 表示);
表示);
(Ⅱ)求总利润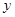 的最大值及相应的
的最大值及相应的 的值.
的值.
已知抛物线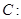
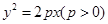 的准线为
的准线为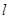 ,焦点为
,焦点为 .⊙M的圆心在
.⊙M的圆心在 轴的正半轴上,且与
轴的正半轴上,且与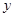 轴相切.过原点
轴相切.过原点 作倾斜角为
作倾斜角为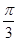 的直线,交
的直线,交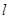 于点
于点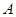 , 交⊙M于另
, 交⊙M于另
一点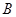 ,且
,且 .
.
(Ⅰ)求⊙M和抛物线 的方程;
的方程;
(Ⅱ)过圆心 的直线交抛物线
的直线交抛物线 于
于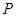 、
、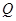 两点,求
两点,求 的值
的值
设数列 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列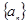 为等差数列,且
为等差数列,且 .
.
(Ⅰ)求数列  的通项公式;
的通项公式;
(Ⅱ)若 ,
,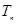 为数列
为数列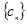 的前
的前 项和,求
项和,求