已知椭圆 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
已知集合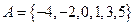 ,在平面直角坐标系中,点
,在平面直角坐标系中,点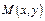 的坐标x∈A,y∈A。计算:
的坐标x∈A,y∈A。计算:
(1)点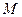 正好在第二象限的概率;
正好在第二象限的概率;
(2)点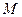 不在x轴上的概率;
不在x轴上的概率;
(3)点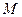 正好落在区域
正好落在区域 上的概率。
上的概率。
已知 ,(Ⅰ)求
,(Ⅰ)求 的值;
的值; (Ⅱ)求
(Ⅱ)求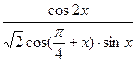 的值
的值
如图,矩形花园ABCD,AB为4米,BC为6米,小鸟任意落下,则小鸟落在阴影区的概率是多少?
两人相约在7点到8点在某地会面,先到者等候另一个人20分钟方可离去. 试求这两人能会面的概率?
袋里装有35个球,每个球上都标有从1到35的一个号码,设号码n的球重 (克).这些球以等可能性(不受重量的影响)从袋里取出.
(克).这些球以等可能性(不受重量的影响)从袋里取出.
(1)如果任意取出一球,试求其重量大于号码数的概率;
(2)如果同时任意取出二球,试求它们重量相同的概率.