已知 .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
命题p:  ,其中
,其中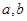 满足条件:五个数
满足条件:五个数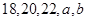 的平均数是20,标准差是
的平均数是20,标准差是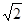 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。试建立适当的直角坐标系,解决下列问题: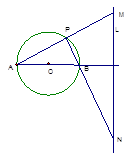
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
已知抛物线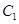 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线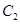 :
: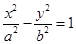 的一个焦点
的一个焦点 且垂直于
且垂直于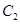 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线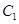 与双曲线
与双曲线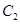 的一个交点是
的一个交点是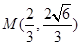 .
.
(1)求抛物线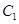 的方程及其焦点
的方程及其焦点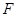 的坐标;
的坐标;
(2)求双曲线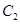 的方程及其离心率
的方程及其离心率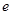 .
.
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
从某校参加2012年全国高中数学联赛预赛的450名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.
(1)根据表中已知数据,你认为在①、②、③处的数值分别为,,.
(2)补全在区间 [70,140] 上的频率分布直方图;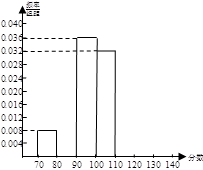
(3)若成绩不低于100分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?