如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.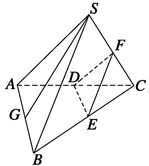
几何证明选讲如图:已知圆上的弧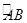 =
=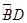 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点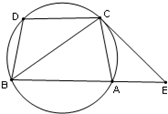
证明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE×CD.
如图: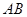 是⊙
是⊙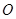 的直径,
的直径,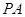 垂直于⊙
垂直于⊙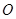 所在的平面,PA="AC,"
所在的平面,PA="AC," 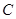 是圆周上不同于
是圆周上不同于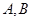 的任意一点,(1) 求证:
的任意一点,(1) 求证: 平面
平面 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。
在等差数列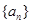 中,
中, ,前
,前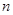 项和为
项和为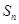 ,等比数列
,等比数列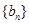 各项均为正数,
各项均为正数, ,且
,且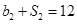 ,
,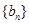 的公比
的公比 .
.
(1)求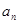 与
与 ;(2)求
;(2)求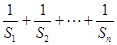 .
.
已知直线 经过点
经过点 ,倾斜角是
,倾斜角是
①求直线 的参数方程
的参数方程
②求直线 与直线
与直线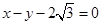 的交点与点
的交点与点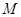 的距离
的距离
③在圆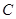 :
: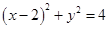 上找一点
上找一点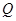 使点
使点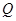 到直线
到直线 的距离最小,并求其最小值。
的距离最小,并求其最小值。
交通管理部门为了优化某路段的交通状况,经过对该路段的长期观测发现:在交通繁忙的时段内,该路段内汽车的车流量 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度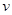 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为
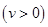
①求在该路段内,当汽车的平均速度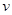 为多少时,车流量最大?最大车流量为多少?(精确到
为多少时,车流量最大?最大车流量为多少?(精确到 千辆/时)
千辆/时)
②若要求在该时段内车流量超过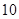 千辆/时,则汽车的平均速度应限定在什么范围内?
千辆/时,则汽车的平均速度应限定在什么范围内?