如图,在四棱锥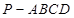 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,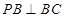 ,
,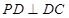 ,且
,且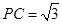 .
.
(Ⅰ)求证: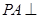 平面
平面 ;
;
(Ⅱ)求二面角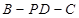 的余弦值;
的余弦值;
(Ⅲ)棱 上是否存在一点
上是否存在一点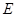 ,使直线
,使直线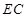 与平面
与平面 所成的角是
所成的角是 ?若存在,求
?若存在,求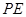 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
已知 、 、 均为正数,证明: ,并确定 、 、 为何值时,等号成立。
已知函数
.
(Ⅰ)讨论函数
的单调性;
(Ⅱ)设
,证明:对任意
,
。
证明以下命题:
(1)对任一正整数
,都存在正整数
,使得
成等差数列;
(2)存在无穷多个互不相似的三角形
,其边长
为正整数且
成等差数列.
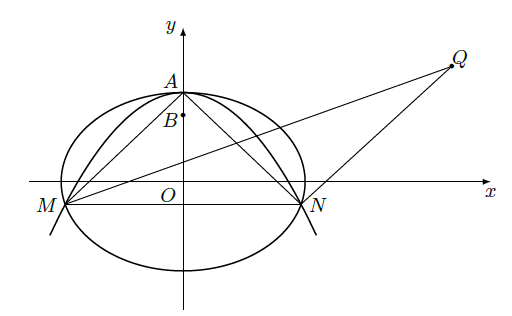
设椭圆 : ,抛物线 : .
(1) 若
经过
的两个焦点,求
的离心率;
(2) 设
,又
为
与
不在
轴上的两个交点,若
的垂心为
,且
的重心在
上,求椭圆
和抛物线
的方程.
如图,
与
都是边长为2的正三角形,
平面
平面
,
平面
,
.
(1)求点
到平面
的距离;
(2)求平面
与平面
所成二面角的正弦值.