如图,在四棱柱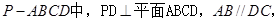

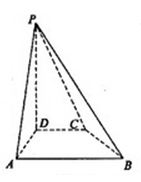
(1)当正视方向与向量 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);
(2)若M为PA的中点,求证:求二面角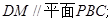
(3)求三棱锥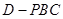 的体积.
的体积.
已知椭圆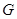 :
: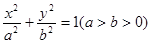 的离心率为
的离心率为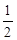 ,过椭圆
,过椭圆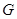 右焦点
右焦点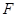 的直线
的直线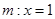 与椭圆
与椭圆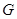 交于点
交于点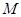 (点
(点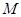 在第一象限).
在第一象限).
(1)求椭圆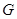 的方程;
的方程;
(2)已知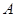 为椭圆
为椭圆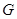 的左顶点,平行于
的左顶点,平行于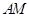 的直线
的直线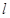 与椭圆相交于
与椭圆相交于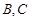 两点.判断直线
两点.判断直线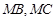 是否关于直线
是否关于直线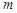 对称,并说明理由.
对称,并说明理由.
如图,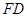 垂直于矩形
垂直于矩形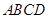 所在平面,
所在平面,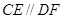 ,
,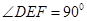 .
.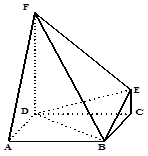
(1)求证: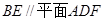 ;
;
(2)若矩形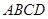 的一个边
的一个边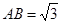 ,
,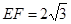 ,则另一边
,则另一边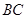 的长为何值时,三棱锥
的长为何值时,三棱锥 的体积为
的体积为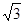 ?
?
从某校高三上学期期末数学考试成绩中,随机抽取了 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下: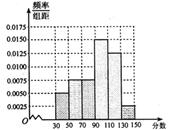
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人中成绩在
人中成绩在 的有几人?
的有几人?
(3)在(2)中抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在 和
和 各
各 人的概率.
人的概率.
在锐角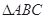 中,角
中,角 所对边分别为
所对边分别为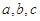 ,已知
,已知 .
.
(1)求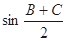 的值;
的值;
(2)若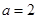 ,
, 求
求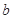 的值.
的值.
(满分12分)已知函数 .
.
(1)当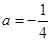 时,求函数
时,求函数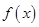 的单调区间;
的单调区间;
(2)若函数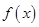 在区间
在区间 上为减函数,求实数
上为减函数,求实数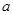 的取值范围;
的取值范围;
(3)当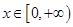 时,不等式
时,不等式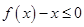 恒成立,求实数
恒成立,求实数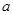 的取值范围.
的取值范围.