某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.
A地区用户满意度评分的频率分布直方图
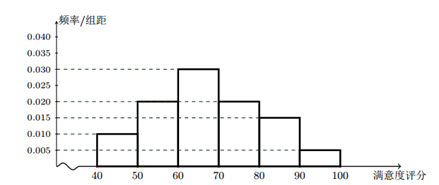
B地区用户满意度评分的频率分布表
| 满意度评分分组 |
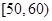 |
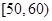 |
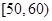 |
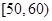 |
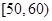 |
| 频数 |
2 |
8 |
14 |
10 |
6 |
(Ⅰ)作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
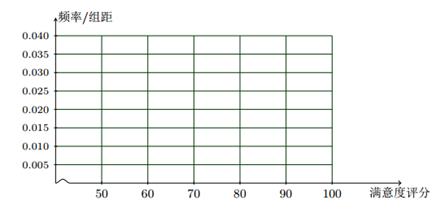
(Ⅱ)根据用户满意度评分,将用户的满意度评分分为三个等级:
| 满意度评分 |
低于70分 |
70分到89分 |
不低于90分 |
| 满意度等级 |
不满意 |
满意 |
非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点。
(1)求AB边所在的直线方程;
(2)求中线AM的长
(3)求AB边的高所在直线方程。
.(本小题满分15分)已知函数 是定义在
是定义在 上的奇函数,
上的奇函数,
当 时,
时, .
.
(Ⅰ)求当 时,函数
时,函数 的表达式;
的表达式;
(Ⅱ)求满足 的
的 的取值范围;
的取值范围;
(Ⅲ)已知对于任意的 ,不等式
,不等式 恒成立,求证:函数
恒成立,求证:函数 的图象与直线
的图象与直线 没有交点.
没有交点.
(本小题满分15分)若函数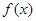 在定义域内存在区间
在定义域内存在区间 ,满足
,满足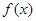 在
在 上的值域为
上的值域为 ,则称这样的函数
,则称这样的函数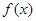 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数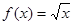 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数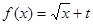 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.
.(本小题满分14分)已知集合 和
和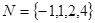 . 设关于x的二次函数
. 设关于x的二次函数 .
.
(Ⅰ)若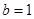 时,从集合
时,从集合 取一个数作为
取一个数作为 的值,求方程
的值,求方程 有解的概率;
有解的概率;
(Ⅱ)若从集合 和
和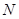 中各取一个数作为
中各取一个数作为 和
和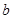 的值,求函数
的值,求函数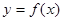 在区间
在区间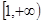 上是增函数的概率.
上是增函数的概率.
(本小题满分14分)
设全集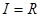 ,已知集合
,已知集合 .
.
(Ⅰ)求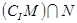 ;(Ⅱ)记集合
;(Ⅱ)记集合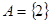 ,已知
,已知 ,
,
若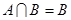 ,求实数
,求实数 的取值范围.
的取值范围.