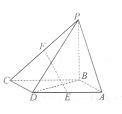
如图,四棱锥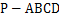 的底面
的底面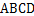 是平行四边形,
是平行四边形,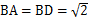 ,
,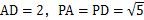 ,
,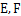 分别是棱
分别是棱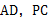 的中点.
的中点.
(1)证明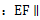 平面
平面 ;
;
(2)若二面角P-AD-B为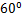 ,
,
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
(本小题12分)下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
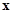 |
2 |
3 |
4 |
5 |
6 |
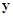 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程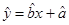 ;
;
(3)估计使用年限为10年时,维修费用为多少?(参考数值:
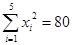 )
)
(参考公式: ;
; ;)
;)
(本小题12分)设各项均为正数的等比数列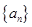 中,
中,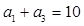 ,
,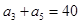 .设
.设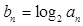
(Ⅰ)求数列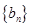 的通项公式;
的通项公式;
(Ⅱ)若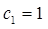 ,
,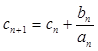 ,求证:
,求证: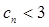 ;
;
(本小题12分)函数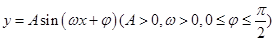 在
在 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当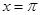 时,
时,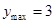 ;当
;当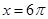 时,
时,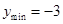 .
.
(Ⅰ)求此函数的解析式;
(Ⅱ)求此函数的单调递增区间.
(本小题10分)命题 :实数
:实数 满足
满足 ,其中
,其中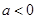 ;命题
;命题 :实数
:实数 满足
满足 或
或 ;若
;若 是
是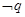 的必要不充分条件,求
的必要不充分条件,求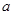 的取值范围.
的取值范围.
已知椭圆 的离心率
的离心率 .直线x=t(t>0)与曲线E交于不同的两点
.直线x=t(t>0)与曲线E交于不同的两点 ,
, ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为 .
.
(1)求椭圆 的方程;
的方程;
(2)若圆 与y轴相交于不同的两点A,B,求△ABC的面积的最大值.
与y轴相交于不同的两点A,B,求△ABC的面积的最大值.