设函数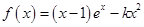 (其中
(其中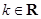 ).
).
(Ⅰ)当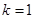 时,求函数
时,求函数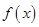 的单调区间;
的单调区间;
(Ⅱ)当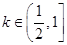 时,求函数
时,求函数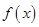 在
在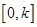 上的最大值
上的最大值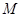 .
.
(本小题满分12分)已知函数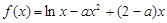 .
.
(1)讨论 的单调性;
的单调性;
(2)设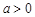 ,证明:当
,证明:当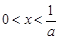 时,
时, ;
;
(3)若函数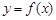 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明: (x0)<0.
(x0)<0.
(本小题12分)设函数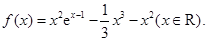
(1)求函数 的单调区间;
的单调区间;
(2)求 在
在 上的最小值;
上的最小值;
(本小题12分)在数列 中,
中, ,
,
(1)计算 并猜想数列
并猜想数列 的通项公式;
的通项公式;
(2)用数学归纳法证明你的猜想。
(本小题满分12分)某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格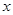 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式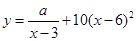 ,其中
,其中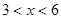 ,
,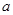 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(1)求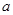 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格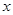 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
(本小题满分12分)在国家法定工作日内,每周满工作量的时间为40小时,若每周工作时间不超过40小时,则每小时工资25元;如因需要加班,超过40小时的每小时工资为50元.某公务员在一周内工作时间为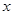 小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资
小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资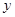 元的算法的程序框图.(注:满工作量外的工作时间为加班)
元的算法的程序框图.(注:满工作量外的工作时间为加班)