选修4-4:坐标系与参数方程
在直角坐标系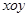 中,曲线
中,曲线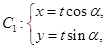 (
(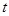 为参数,
为参数,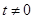 ),其中
),其中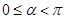 ,在以
,在以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线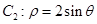 ,曲线
,曲线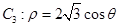 .
.
(Ⅰ).求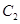 与
与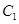 交点的直角坐标;
交点的直角坐标;
(Ⅱ).若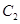 与
与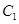 相交于点
相交于点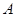 ,
,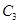 与
与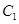 相交于点
相交于点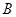 ,求
,求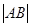 的最大值.
的最大值.
已知椭圆 的焦点在
的焦点在 轴上,长轴长为
轴上,长轴长为 ,离心率为
,离心率为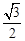 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点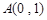 和直线
和直线 :
: ,线段
,线段 是椭圆
是椭圆 的一条弦且直线
的一条弦且直线 垂直平
垂直平
分弦 ,求实数
,求实数 的值.
的值.
已知 是函数
是函数 的一个极值点.
的一个极值点.


(1)求 的值;
的值;
(2)求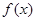 在区间
在区间 上的最值.
上的最值.
已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.
(1)求椭圆方程;
(2)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段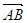 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
在直角梯形PBCD中,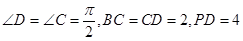 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。
(1)求证: 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
在平面直角坐标系 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 相交于A、B两点。
相交于A、B两点。
(1)求证:命题“如果直线 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。