某蔬菜加工厂承担出口蔬菜加工任务，有一批蔬菜产品需要装入某一规格的纸箱．供应这种纸箱有两种方案可供选择：
方案一：从纸箱厂定制购买，每个纸箱价格为4元；
方案二：由蔬菜加工厂租赁机器自己加工制作这种纸箱，工厂需要一次性投入机器租赁、安装等费用16000元，每加工一个纸箱还需成本费2．4元．
（1）若需要这种规格的纸箱
个，请分别写出从纸箱厂购买纸箱的费用y（元）和蔬菜加工厂自己加工制作纸箱的费用y2（元）关于（个）的函数关系式；
（2）假设你是决策者，你认为应该选择哪种方案？并说明理由．
如
图，△ABC中，AD是边BC上的高，CF是边AB上的中线，且DC＝BF，DE⊥CF于E.
E是CF的中点吗？试说明理由
试说明：∠B＝2∠BCF
情景一：如图(1)中AC=40m，CB=30m，从教室楼到宿舍楼，总有少数同学不走人行道AC和BC，而直接横穿草坪（即从A到B），你认为他们这样走，近了多少米？说明理由.
情景二：M、N是河流l旁的两个村庄，现要在河边修一个抽水站向M、N村供水，问抽水站修在什么地方才能使所需的管道最短？请在图(2)中画出抽水站点P的位置．（保留作图痕迹，不写作法）
数学知识来源于生活并且用来为人们服务，上面两个情景你赞同哪一个
？你有何感想？（简要说明）
如图，在平行四边形ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．
试说明：AE∥CF
连接AF和CE，试说明四边形AFCE是平行四边形．
如图
，在梯形ABCD中，AB∥DC，AD=BC，点E是CD延长线上一点，且AE∥BD．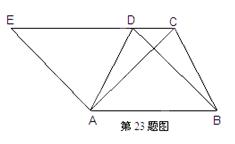
判断四边形A
BDE是怎样的四边形，说明理由△ACE是等腰三角形吗？请说明理由
如图，在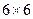
的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形．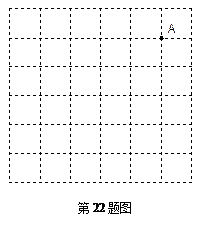
从点A出发的一条线段AB，使它的另一个端点落在格点（即小正方形的顶点）上，且长度为
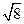
以（1）中的AB为边的一个等腰ABC，使点C在格点上，且另两边的长都是无理数（画出一个符合条件的三角形即可）
画出（2）中△ABC关于点B的中心对称图形△A1BC1.