如图,直线l上有A、B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.

(1)OA= cm,OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为ts.当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
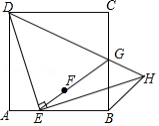
如图,在正方形 中, 是边 上的一动点(不与点 、 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .
(1)求证: ;
(2)用等式表示线段 与 的数量关系,并证明.
在平面直角坐标系 中,直线 与 轴, 轴分别交于点 , ,抛物线 经过点 ,将点 向右平移5个单位长度,得到点 .
(1)求点 的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段 恰有一个公共点,结合函数图象,求 的取值范围.
某年级共有300名学生.为了解该年级学生
,
两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.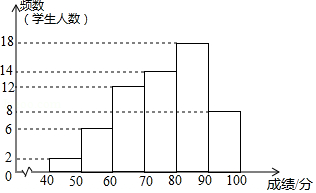
. 课程成绩的频数分布直方图如下(数据分成6组: , , , , ,
. 课程成绩在 这一组的是:70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
. , 两门课程成绩的平均数、中位数、众数如下:
|
课程 |
平均数 |
中位数 |
众数 |
|
|
75.8 |
|
84.5 |
|
|
72.2 |
70 |
83 |
根据以上信息,回答下列问题:
(1)写出表中 的值;
(2)在此次测试中,某学生的 课程成绩为76分, 课程成绩为71分,这名学生成绩排名更靠前的课程是 (填“ ”或“ ” ,理由是 ,
(3)假设该年级学生都参加此次测试,估计 课程成绩超过75.8分的人数.
如图, 是 与弦 所围成的图形的内部的一定点, 是弦 上一动点,连接 并延长交 于点 ,连接 .已知 ,设 , 两点间的距离为 , , 两点间的距离为 , , 两点间的距离为 .
小腾根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值;
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
|
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
(2)在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点 , ,并画出函数 , 的图象;

(3)结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .

在平面直角坐标系 中,函数 的图象 经过点 ,直线 与图象 交于点 ,与 轴交于点 .
(1)求 的值;
(2)横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .
①当 时,直接写出区域 内的整点个数;
②若区域 内恰有4个整点,结合函数图象,求 的取值范围.