如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形.除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为 ,其中
,其中 (
( ),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为
),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为 .
.
(1)当k=4时,若要求 为2的倍数,则有多少种不同的标注方法?
为2的倍数,则有多少种不同的标注方法?
(2)当k=11时,若要求 为3的倍数,则有多少种不同的标注方法?
为3的倍数,则有多少种不同的标注方法?
三、解答题
18、(本小题满分14分)已知函数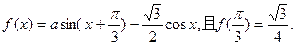
(I)求实数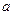 的值;(II)求
的值;(II)求 的最小正周期和单调增区间。
的最小正周期和单调增区间。
(本小题满分14分) 设函数
设函数 ,函数
,函数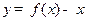 有唯一的零点,其中实数
有唯一的零点,其中实数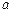 为常数,
为常数, ,
,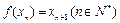 .
.
(Ⅰ)求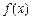 的表达式;(Ⅱ)求
的表达式;(Ⅱ)求 的值;
的值;
(Ⅲ)若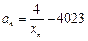 且
且 ,求证:
,求证: .
.
(本小题满分13分)
设点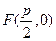 (
(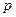 为正常数),点
为正常数),点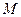 在
在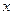 轴的负半轴上,点
轴的负半轴上,点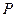 在
在 轴上,且
轴上,且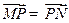 ,
, .
.
(Ⅰ)当点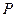 在
在
 轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)直线 过点
过点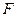 且与曲线
且与曲线 相交于不同两点
相交于不同两点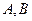 ,分别过点
,分别过点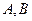 作直线
作直线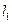 :
: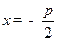 的
的 垂线,对应的垂足分别为
垂线,对应的垂足分别为
 ,求
,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,记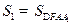 ,
, ,
,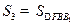 ,
,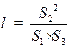 ,求
,求 的值.
的值.
(本小题满分12分)
已知函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当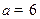 ,
, 时,求函数
时,求函数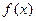 的单调递增区间;
的单调递增区间;
(Ⅱ)若任取 ,
,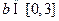 ,求函数
,求函数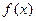 在
在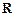 上是增函数的概率.
上是增函数的概率.
在棱长为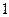 的正方体
的正方体 中,
中,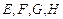 分别是棱
分别是棱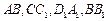 的中点.
的中点.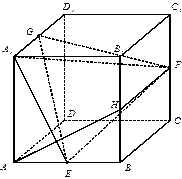
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明: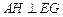 ;
;
(Ⅲ)求三棱锥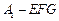 的体积.
的体积.