如图,已知某市一座电视塔高AB为600米.张明在点C处测得电视塔塔顶B的仰角∠ACB=40°。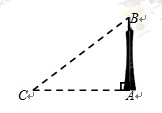
(1)求∠B的度数;
(2)求AC的长(精确到1米).
如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上.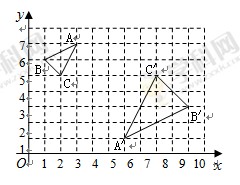
(1)在图上找出位似中心P的位置,并直接写出点P的坐标是;
(2)写出△ABC与△A′B′C′的面积比.
解方程: .
.
在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
某服装商店用9600元购进了某种时装若干套,第一个月每套按进价增加30%作为售价,售出了100套,第二个月换季降价处理,每套比进价低10元销售,售完了余下的时装,结果在买卖这种服装的过程中共盈利2200元,求每套时装的进价.