选修4-4:极坐标与参数方程
在极坐标系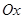 中,直线
中,直线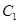 的极坐标方程为
的极坐标方程为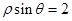 ,
,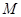 是
是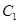 上任意一点,点
上任意一点,点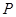 在射线
在射线 上,且满足
上,且满足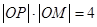 ,记点
,记点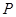 的轨迹为
的轨迹为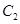 .
.
(1)求曲线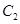 的极坐标方程;
的极坐标方程;
(2)求曲线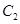 上的点到直线
上的点到直线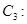
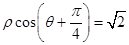 的距离的最大值.
的距离的最大值.
(本题15分)已知集合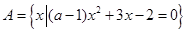 ,
,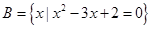
(1)若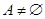 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若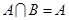 ,求实数
,求实数 的取值范围.
的取值范围.
(本题14分)某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数: (其中x是仪器的月产量).
(其中x是仪器的月产量).
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
(本题14分)设集合
 ,集合
,集合 ,
,
(1)若 ,求
,求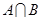 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(本题18分)已知函数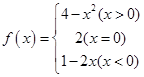 ,
,
(1)画出函数 图像;
图像;
(2)求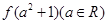 ,
,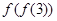 的值;
的值;
(3)当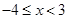 时,求
时,求 取值的集合.
取值的集合.
(本题18分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?