已知命题 曲线
曲线 与
与 轴相交于不同的两点;命题
轴相交于不同的两点;命题 表示焦点在
表示焦点在 轴上的椭圆,.若“
轴上的椭圆,.若“ 且
且 ”是假命题,“
”是假命题,“ 或
或 ”是真命题,求
”是真命题,求 的取值范围.
的取值范围.
设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足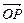 ·
·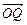 =0.
=0.
(1)求m的值;
(2)求直线PQ的方程.
甲、乙两地相距s ( km ),汽车从甲地匀速行驶到乙地,速度不得超过c ( km/h ),已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 的平方成正比,比例系数为2, 固定部分为3000元.
的平方成正比,比例系数为2, 固定部分为3000元.
(1)把全程运输成本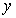 (元)表示为速度
(元)表示为速度 的函数。
的函数。
(2)为了使全程运输成本最小,汽车应以多大的速度行驶?并求最小运输成本。
在ΔABC中,角A、B、C所对的边分别为a、b、c,且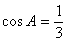 .
.
(1)求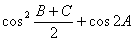 的值;
的值;
(2)若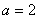 ,
, ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.
已知函数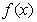 是定义在
是定义在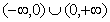 上的偶函数,当
上的偶函数,当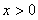 时,
时,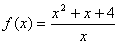
(1)求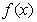 的解析式.
的解析式.
(2)讨论函数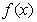 的单调性,并求
的单调性,并求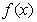 的值域.
的值域.
(文)(本大题满分12分)
掷一枚硬币,正、反两面出现的概率都是0.5,把这枚硬币反复掷8次,这8次中的第n次中,假若正面出现,记an=1,若反面出现,记an=-1,令Sn=a1+a2+…+an(1≤n≤8),在这种情况下,试求下面的概率:
(1)S2≠0且S8=2的概率;
(2)S4=0且S8=2的概率.