某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作-优题课

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

零件的个数（个）	2	3	4	5
加工的时间（小时）	2．5	3	4	4．5

（1）求出关于的线性回归方程，并在坐标系中画出回归直线；

（2）试预测加工个零件需要多少小时？
（注：，，，）

科目数学题型解答题难度困难

已知等差数列 ${a_{n}}$ 的前n项和为S_n，等比数列 ${b_{n}}$ 的前n项和为T_n， $a_{1} ＝﹣ 1$ ， $b_{1} ＝ 1$ ， $a_{2} + b_{2} ＝ 2$ ．

（1）若 $a_{3} + b_{3} ＝ 5$ ，求 ${b_{n}}$ 的通项公式；

（2）若 $T_{3} ＝ 21$ ，求S₃．

已知函数 $f （ x ）＝ |x + 1| ﹣ | 2 x ﹣ 3 |$ ．

（Ⅰ）在图中画出 $y ＝ f （ x ）$ 的图象；

（Ⅱ）求不等式 $| f （ x ） | ＞ 1$ 的解集．

在直角坐标系 $xOy$ 中，曲线C₁的参数方程为 $\{\begin{matrix} x = a \cos t \\ y = 1 + asint \end{matrix}$ （t为参数， $a ＞ 0$ ）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线 $C_{2} ： ρ ＝ 4 cosθ$ ．

（Ⅰ）说明C₁是哪种曲线，并将C₁的方程化为极坐标方程；

（Ⅱ）直线C₃的极坐标方程为 $θ ＝ α_{0}$ ，其中α₀满足 $\tan α_{0} ＝ 2$ ，若曲线C₁与C₂的公共点都在C₃上，求a．

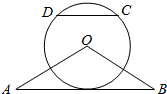
如图，△OAB是等腰三角形， $∠ AOB ＝ 120 °$ ．以O为圆心， $\frac{1}{2} OA$ 为半径作圆．

（Ⅰ）证明：直线AB与⊙O相切；

（Ⅱ）点C，D在⊙O上，且A，B，C，D四点共圆，证明： $AB ∥ CD$ ．

已知函数 $f （ x ）＝（ x - 2 ） e^{x} + a （ x - 1 ）^{2}$ ．

（Ⅰ）讨论 $f （ x ）$ 的单调性；

（Ⅱ）若 $f （ x ）$ 有两个零点，求a的取值范围．

试卷网试题网古诗词网作文网范文网