某公司计划2015年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元．甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，假定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0．3万元和0．2万元，问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大?最大收益是多少万元?
已知一个数列
的各项都是1或2．首项为1，且在第
个1和第
个1之间有
个2，即1，2，1，2，2，2，1，2，2，2，2，2，1，…．记数列的前
项的和为
．
参考：31×32=992，32×33＝1056，44×45=1980，45×46=2070，2011×2012＝4046132
（１）试问第2012个1为该数列的第几项？
（２）求
和
；
（３）（特保班做）是否存在正整数
，使得
？如果存在,求出的值；如果不存在,请说明理由．
甲、乙两人进行乒乓球单打比赛，比赛规则为：七局四胜制，每场比赛均不出现平局.假设两人在每场比赛中获胜的概率都为
．
(1) 求需要比赛场数
的分布列及数学期望
；
(2) 如果比赛场馆是租借的，场地租金
元，而且每赛一场追加服务费
元，那么举行一次这样的比赛，预计平均花费多少元？
已知
为实数，证明：
．
已知函数
，
．
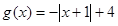（１）若函数
的值不大于
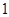，求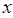
的取值范围；
（２）若不等式
的解集为
，求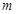
的取值范围．
在直角坐标系
内，直线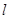
的参数方程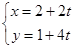
（
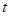为参数），以
为极轴建立极坐标系，圆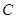
的极坐标方程为
．
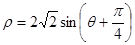（１）求直线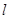的普通方程和圆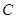的直角坐标方程；
（２）确定直线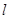和圆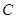的位置关系．