在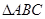 中,三个内角
中,三个内角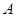 ,
,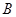 ,
,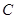 的对边分别为
的对边分别为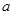 ,
,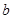 ,
,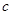 ,其中
,其中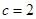 ,且
,且
(1)求证: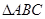 是直角三角形;
是直角三角形;
(2)设圆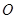 过
过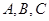 三点,点
三点,点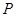 位于劣弧
位于劣弧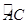 上,
上,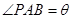 ,用
,用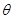 的三角函数表示三角形
的三角函数表示三角形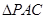 的面积,并求
的面积,并求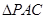 面积最大值.
面积最大值.
设命题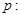 函数
函数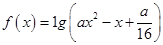 的定义域为
的定义域为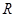 ;命题
;命题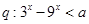 对一切的实数
对一切的实数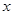 恒成立,如果命题“
恒成立,如果命题“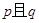 ”为假命题,求实数
”为假命题,求实数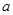 的取值范围.
的取值范围.
设函数 (m>0)
(m>0)
(1)证明:f(x)≥4;
(2)若f(2)>5,求m的取值范围.
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
(1)求证:AT2=BT·AD;
(2)E、F是BC的三等分点,且DE=DF,求∠A.