如图,抛物线y=ax2+bx﹣ 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.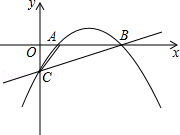
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.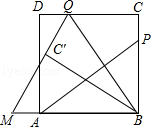
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF.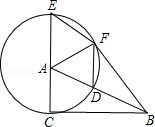
(1)求证:△ABC≌△ABF;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)