2015年国家实施“全面二孩政策”,人民医院迎来人口出生小高峰,某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是多少?画出树状图或列表。
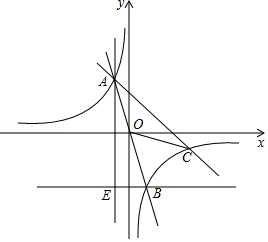
如图,反比例函数 与一次函数 的图象在第二象限的交点为 ,在第四象限的交点为 ,直线 为坐标原点)与函数 的图象交于另一点 .过点 作 轴的平行线,过点 作 轴的平行线,两直线相交于点 , 的面积为6.
(1)求反比例函数 的表达式;
(2)求点 , 的坐标和 的面积.
期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.
(1)求购买一个甲种、一个乙种笔记本各需多少元?
(2)两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的 ,求至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.
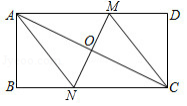
如图,在矩形 中, 为对角线 的中点,过点 作直线分别与矩形的边 , 交于 , 两点,连接 , .
(1)求证:四边形 为平行四边形;
(2)若 , ,且 ,求 的长.
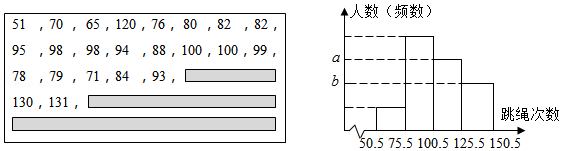
为了了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如图的频数直方图,图中的 , 满足关系式 .后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)求问题中的总体和样本容量;
(2)求 , 的值(请写出必要的计算过程);
(3)如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数大约是多少人?(注:该年级共1000名学生)
如图, , 为两个建筑物,两建筑物底部之间的水平地面上有一点 ,从建筑物 的顶点 测得 点的俯角为 ,从建筑物 的顶点 测得 点的俯角为 ,测得建筑物 的顶点 的俯角为 .若已知建筑物 的高度为20米,求两建筑物顶点 、 之间的距离(结果精确到 ,参考数据: , .
