阅读课本材料，解答后面的问题．
折纸与证明
折纸，常常能为证明一个命题提供思路和方法．例如，在△ABC中，AB＞AC（图27－1），怎样证明∠C＞
∠B呢？
把AC沿∠A的平分线AD翻折，因为AB＞AC，所以，点C落在AB上的点C’处（图27－2）．于是，由∠AC’D＞∠B，可得∠C＞∠B．
在△ABC中，∠B=2∠C，点D为线段BC上一动点，当AD满足某种条件时，探讨在线段AB、BD、CD、AC四条线段中，某两条或某三条线段之间存在的数量关系．
（1）如图3，当AD⊥BC时，求证：AB+BD=DC；
（2）如图4，当AD是∠BAC的角平分线时，写出AB、BD、AC的数量关系，并证明．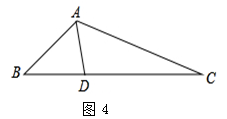
(本小题满分8分)
某中学开展“唱红歌”比赛活动，九年级(1)、(2)班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分为i00分)如图所示．
(1)根据图示填写下表；
(2)结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
(3)计算两班复赛成绩的方差。
(本小题满分8分)如图，某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度，他们先在A处测得古塔顶端点D的仰角为45°，再沿着BA的方向后退20m至C处，测得古塔顶端点D的仰角为30°。求该古塔BD的高度（
，结果保留一位小数）。
(本题共两小题．每小题6分．满分l2分)
（1）计算：
（2）求满足不等式组的
整数解。
已知抛物线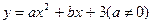
经过A(3，0), B(4，1)两点，且与y轴交于点C．
（1）求抛物线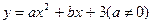的函数关系式及点C的坐标；
（2）如图（1）,连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图（2）,连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标．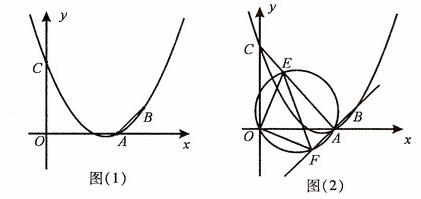
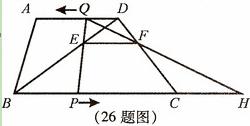
如图，梯形ABCD中，AD∥BC，BC＝20cm，AD＝10cm，现有两个动点P、Q
分别从B、D两点同时出发，点P以每秒2cm的速度沿BC向终点C移动，点Q以每秒1cm
的速度沿DA向终点A移动，线段PQ与BD相交于点E，过E作EF∥BC交CD于点F，射线
QF交BC的延长线于点H，设动点P、Q移动的时间为t（单位：秒，0<t<10）．
（1）当t为何值时，四边形PCDQ为平行四边形？
（2）在P、Q移动的过程中，线段PH的长是否发生改变？如果不变，求出线段PH的长；如果改变，请说明理由．