(本小题满分8分)
某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为i00分)如图所示.
(1)根据图示填写下表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差。
如图,已知锐角 的面积为 ,正方形 是 的一个内接四边形, ,求正方形 面积的最大值.
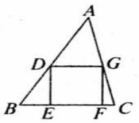
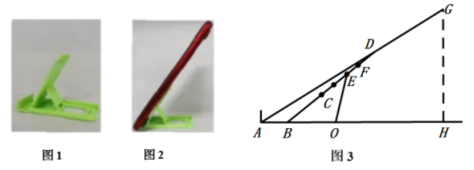
图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 ,托架斜面长 ,它有 到 共4个挡位调节角度,相邻两个挡位间的距离为 ,挡位 到 的距离为 .将某型号手机置于托架上(图2,手机屏幕长 是 , 是支点且 (支架的厚度忽略不计).求:
(1)当支架调到 挡时,点 离水平面的距离 为多少厘米;
(2)当支架从 挡调到 挡时,点 离水平面的距离下降了多少厘米.
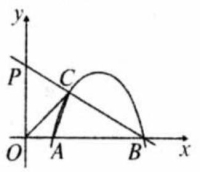
如图,开口向下的抛物线 与 轴交于 两点,抛物线上另有一点 在第一象限,且使 .
(1)求 的长及 的值;
(2)设直线 与 轴交于 点,点 是 的中点时,求直线 和抛物线的解析式.
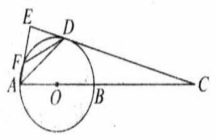
如图,点 在以 为直径的 上,过 作 的切线交 的延长线于点 于点 ,交 于点 ,连接 .
(1)求证:
(2)求证: ;
(3)若 ,求 的长.
如图,在平面直角坐标系 中,抛物线 与两坐标轴分别相交于 三点.
(1)求证: ;
(2)点 是第一象限内该抛物线上的动点,过点 作 轴的垂线交 于点 ,交 轴于点 .
①求 的最大值;
②点 是 的中点,若以点 为顶点的三角形与 相似,求点 的坐标.
