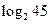以平面直角坐标系的原点为极点,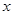 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点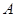 的极坐标为
的极坐标为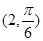 ,直线
,直线 过点
过点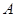 且与极轴成角为
且与极轴成角为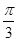 ,圆
,圆 的极坐标方程为
的极坐标方程为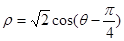 .
.
(1) 写出直线 参数方程,并把圆
参数方程,并把圆 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2) 设直线 与曲线圆
与曲线圆 交于
交于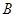 、
、 两点,求
两点,求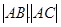 的值.
的值.
(满分17分)
已知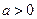 ,函数
,函数 .
.
(1)当 时,求所有使
时,求所有使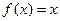 成立的
成立的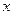 的值;
的值;
(2)当 时,求函数
时,求函数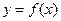 在闭区间
在闭区间 上的最大值和最小值;
上的最大值和最小值;
(3) 试讨论函数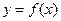 的图像与直线
的图像与直线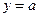 的交点个数.
的交点个数.
(满分15分)
设函数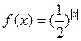 ,
,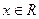
(1)请画出函数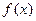 的大致图像;
的大致图像;
(2)若不等式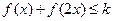 对于任意的
对于任意的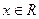 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(满分10分)
已知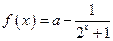 ,其中
,其中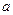 为常数
为常数
(1)判断 在定义域上的单调性并用单调性的定义证明之;
在定义域上的单调性并用单调性的定义证明之;
(2)若函数的定义域为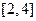 ,求函数的最大值和最小值.
,求函数的最大值和最小值.
(满分10分)
某汽车销售公司以每台10万元的价格销售某种品牌的汽车,可售出该品牌汽车1000台,若将该品牌汽车每台的价格上涨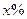 ,则销售量将减少
,则销售量将减少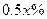 ,且该品牌汽车每台的价格上涨幅度不超过
,且该品牌汽车每台的价格上涨幅度不超过 ,问当该品牌汽车每台的价格上涨百分之几,可使销售的总金额最大?
,问当该品牌汽车每台的价格上涨百分之几,可使销售的总金额最大?
(本大题共2个小题,每小题5分,共10分)
(1)若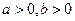 ,化简:
,化简: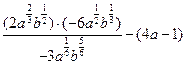
(2)若 ,
, ,试用
,试用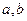 表示
表示