已知中心在原点,焦点在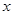 轴的椭圆过点
轴的椭圆过点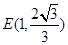 ,且焦距为2,过点
,且焦距为2,过点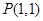 分别作斜率为
分别作斜率为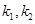 的椭圆的动弦
的椭圆的动弦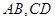 ,设
,设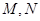 分别为线段
分别为线段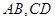 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若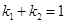 ,求证:直线
,求证:直线 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
(本小题满分13分)
如图,已知椭圆 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形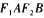 是边长为2的正方形.
是边长为2的正方形.
(I)求椭 圆的方程;
圆的方程;
(II)若C、D分别是椭圆长轴的左、右端点,动点M满足MD丄CD,连结CM,交椭圆于点P.证明: 为定值;
为定值;
(III)在(II)的条件下,试问X轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒 过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.
过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.
(本小题满分12分)
已知数列 中,
中,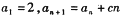 (其中c为非零常数,
(其中c为非零常数,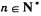 ),
),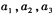 组成公比不为1的等比数列.
组成公比不为1的等比数列.
(I)求c的值;
(II)记数列 的前项和为
的前项和为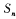 ,求证
,求证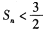
(本小题满分12分)
如图,在四棱锥P - ABCD中,ΔPCD为等边三角形,四边形ABCD为矩形,平面PDC丄平面ABCD,M,N、E分别是AB,PD,PC的中点,AB =2AD.
(I)求证DE丄MN;
(II)求二面角B-PA-D的余弦值.
(本小题满分12分)
有甲、乙两种味道和颜色都极为相似的名酒各4杯.从中挑出4杯称为一次试验,如果能将甲种酒全部挑出来,算作试验成功一次.某人随机地去挑,求:
(I )试验一次就成功的概率是多 少?
少?
(II)恰好在第三次试验成功的概率是多少?
(m)当试验成功的期望值是2时,需要进行多少次相互独立试验?
(本小题满分12分)
已知函数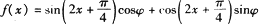 (其中
(其中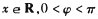 )的图象关于直线x=
)的图象关于直线x= 对称.
对称.
(I)求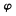 的值;
的值;
(II)求函数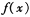 在区间【
在区间【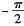 ,O】上的最小值.
,O】上的最小值.