如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
CD.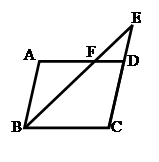
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形的面积.
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
解不等式组:
已知点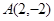 和点
和点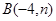 在抛物线
在抛物线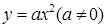 上.
上. 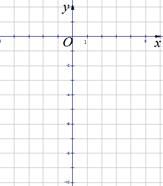
(1)求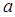 的值及点
的值及点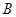 的坐标;
的坐标;
(2)点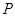 在
在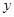 轴上,且满足△
轴上,且满足△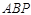 是以
是以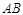 为直角边的直角三角形,求点
为直角边的直角三角形,求点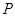 的坐标;
的坐标;
(3)平移抛物线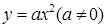 ,记平移后点A的对应点为
,记平移后点A的对应点为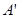 ,点B的对应点为
,点B的对应点为 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,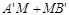 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.
将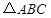 绕点
绕点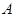 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为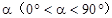 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的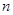 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[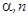 ].
].
(1)如图①,对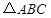 作变换[
作变换[ ]得
]得 ,则
,则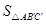 :
: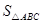 = ___;直线
= ___;直线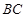 与直线
与直线 所夹的锐角为 __°;
所夹的锐角为 __°;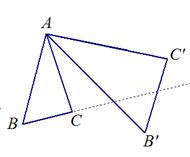
图①
(2)如图②,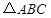 中,
中, ,对
,对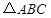 作变换[
作变换[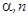 ]得
]得 ,使得四边形
,使得四边形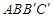 为梯形,其中
为梯形,其中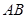 ∥
∥ ,且梯形
,且梯形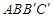 的面积为
的面积为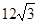 ,求
,求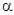 和
和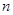 的值.
的值.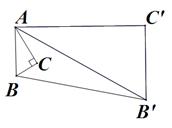
图②
如图,二次函数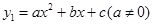 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于 ,
, 两点. C
两点. C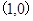 为二次函数图象的顶点.
为二次函数图象的顶点.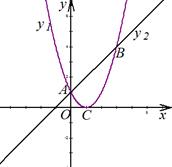
(1)求二次函数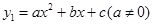 的解析式;
的解析式;
(2)定义函数f:“当自变量x任取一值时,x对应的函数值分别为y1或y2,若y1≠y2,函数f的函数值等于y1、y2中的较小值;若y1=y2,函数f的函数值等于y1(或y2).” 当直线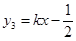 (k >0)与函数f的图象只有两个交点时,求
(k >0)与函数f的图象只有两个交点时,求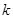 的值.
的值.