探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？
（本小题满分12分）我们新定义一种三角形：两边平方和等于第三边平方的两倍的三角形叫做奇异三角形．
（1）根据“奇异三角形”的定义，请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
（2）在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b>a，若Rt△ABC是奇异三角形，求a：b：c；
（3）如图，AB是⊙O的直径，C是⊙O上一点（不与点A，B重合），D是半圆
的中点，C，D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．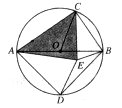
①求证：△ACE是奇异三角形；
②当△ACE是直角三角形时，求∠AOC的度数．
（本小题满分12分）点P为抛物线y=x2-2mx+m2（m为常数，m>0）上任一点，将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A，B两点（点A在点B的上方），点Q为点P旋转后的对应点．
（1）当m=2，点P横坐标为4时，求Q点的坐标；
（2）设点Q（a，b），用含m，b的代数式表示a；（直接写出结果）
（3）如图，点Q在第一象限内，点D在并轴的正半轴上，点C为OD的中点，QD平分∠AQC，AQ=2QC，当QD=m时，求m的值．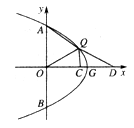
（本小题满分10分）如图，⊙O是△ABC的外接圆，AB=AC=10，BC=12，P是圆上的一个动点，过点P作BC的平行线交AB的延长线于点D．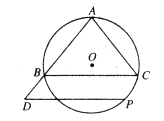
（1）当点P在什么位置时，DP是⊙O的切线?请说明理由；
（2）当DP为⊙O的切线时，求线段DP的长．
（本小题满分10分）某商店第一次用600元购进某种铅笔若干支，第二次又用600元购进该种铅笔，但这次每支的进价比第一次贵l元，所以购进数量比第一次少了30支．
（1）求第一次每支铅笔的进价及购进的数量；
（2）若将这两次购进的铅笔按同一单价x（元，支）全部销售完毕，并要求获利不低于420元，求获利y（元）关于单价x（元／支）的函数关系式及定义域，并在直角坐标系内画出它的大致图象．
（本小题满分10分）已知：如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC=CD，BE⊥CD，垂足为点E，点F在BD上，连接AF，EF．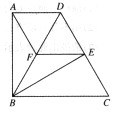
（1）求证：AD=ED；
（2）如果AF∥CD，求证：四边形ADEF是菱形．