先观察下列等式,再回答问题:
①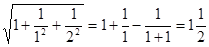 ;
;
②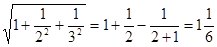 ;
;
③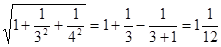 .
.
(1)根据上面三个等式提供的信息,请你猜想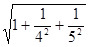 的结果;
的结果;
(2)请按照上面各等式反映的规律,试写出用字母表示的等式.
(年湖南怀化10分)如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.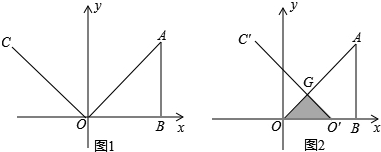
(年新疆区、兵团12分)如图,直线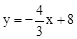 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).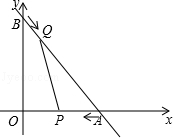
(1)写出A,B两点的坐标;
(2)设△AQP的面积为S,试求出S与t之间的函数关系式;并求出当t为何值时,△AQP的面积最大?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.
(年重庆市B12分)如图1,在□ABCD中,AH⊥DC,垂足为H,AB= ,AD=7,AH=
,AD=7,AH=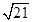 .现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
.现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
(1)求线段AC的长;
(2)在整个运动过程中,设等边△EFG与△ABC重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)当等边△EFG的顶点E到达点C时,如图2,将△EFG绕着点C旋转一个角度 . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.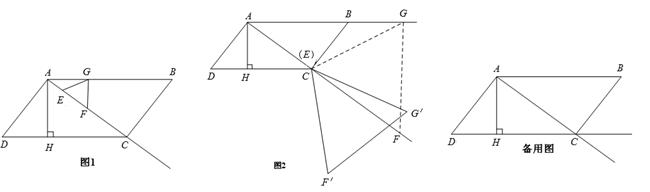
(年四川巴中12分)如图,在平面直角坐标系xOy中,抛物线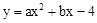 与x轴交于点A
与x轴交于点A
(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.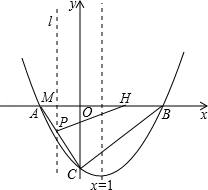
(1)求抛物线的解析式;
(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原
点时,点H立刻掉头并以每秒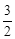 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
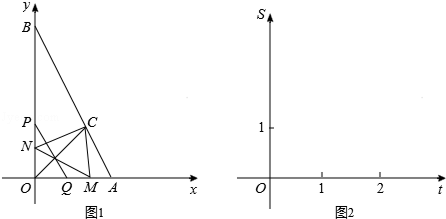
(年江苏无锡10分)如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.