（年新疆区、兵团12分）如图，直线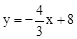
与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）（0＜t≤3）．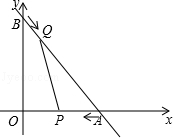
（1）写出A，B两点的坐标；
（2）设△AQP的面积为S，试求出S与t之间的函数关系式；并求出当t为何值时，△AQP的面积最大？
（3）当t为何值时，以点A，P，Q为顶点的三角形与△ABO相似，并直接写出此时点Q的坐标．
在一个不透明的盒子中放有两个红球和一个白球，这三个球除了颜色之外，其他都一样.闭着眼睛从盒子中抽取一个球，不放回，再抽取第二个球.求抽出的两球颜色相同的概率
甲乙两人打算做个游戏，规则如下：如果抽出的两球颜色相同则甲赢，如果颜色不同则乙赢.请说明游戏是否公平.
计算
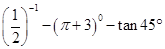
如图3，已知线段
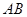，请用直尺和圆规作出线段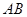的垂直平分线．
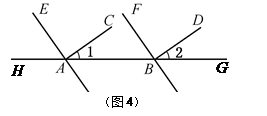
如图4，已知
，
，
，
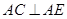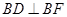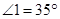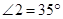.求证：
.
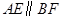如图，一条直线与反比例函数
的图象交于A（1，4）．B（4，n）两点，与
轴交于D点，AC⊥轴，垂足为C．如图甲，①求反比例函数的解析式；②求n的值及D点坐标.
如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF的理由.
②当△ECF为等腰三角形时，直接写出F点坐标． 
先阅读下面解方程
的过程，然后回答后面的问题。
解：将原方程整理为：
（第一步）
方程两边同除以（x－1）得：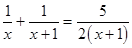 
（第二步）
去分母，得：2（x＋1）＋2x=5x（第三步）
解这个方程，得：x=2（第四步）
在上面的解题过程中：第三步变形的依据是
出现错误的一步是
上述解题过程缺少的一步是
写出这个方程的完整的解题过程
如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上(与A、C不重合)，Q在BC上．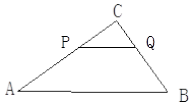
当△PQC的面积是四边形PABQ的面积
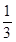时，求CP的长当△PQC的周长与四边形PABQ的周长相等时，求CP的长．