定义在D上的函数f(x),如果满足对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界,已知函数f(x)=1+x+ax2
(1)当a=﹣1时,求函数f(x)在(﹣∞,0)上的值域,判断函数f(x)在(﹣∞,0)上是否为有界函数,并说明理由;
(2)若函数f(x)在x∈[1,4]上是以3为上界的有界函数,求实数a的取值范围.
. (本题满分12分)
已知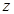 为虚数,且
为虚数,且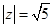 ,
,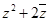 为实数,求复数
为实数,求复数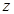 .
.
(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是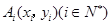 ,(如图所示,
,(如图所示,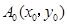 坐标以已知条件为准),
坐标以已知条件为准),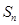 表示青蛙从点
表示青蛙从点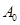 到点
到点 所经过的路程。
所经过的路程。
(1) 若点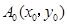 为抛物线
为抛物线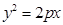
 准线上
准线上
一点,点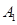 ,
,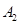 均在该抛物线上,并且直线
均在该抛物线上,并且直线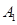
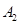 经
经
过该抛物线的焦点,证明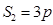 .
.
(2)若点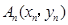 要么落在
要么落在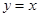 所表示的曲线上,
所表示的曲线上,
要么落在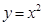 所表示的曲线上,并且
所表示的曲线上,并且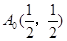 ,
,
试写出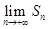 (不需证明);
(不需证明);
(3)若点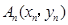 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在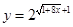 所表示的曲线上,并且
所表示的曲线上,并且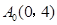 ,求
,求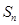 的表达式.
的表达式.
.(本题满分16分,其中第1小题4分,第2小题6分,第3小题6分,)
如图,已知椭圆 ,
, ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点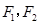 为顶点的三角形的周长为
为顶点的三角形的周长为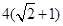 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设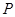 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和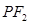 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
(1)求椭圆和双曲线的标准方程;
(2)设直线 、
、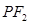 的斜率分别为
的斜率分别为 、
、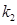 ,证明
,证明 ;
;
(3)是否存在常数 ,使得
,使得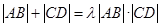
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.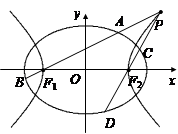
(本题满分14分,其中第1小题6分,第2小题8分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度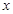 (单位:cm)满足关系:
(单位:cm)满足关系: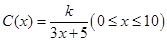 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设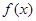 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及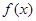 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用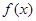 达到最小,并求最小值.
达到最小,并求最小值.
(本题满分14分,其中第1小题6分,第2小题8分)
在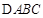 中,
中, 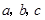 分别为角
分别为角 的对边,且满足
的对边,且满足 .
.
(1)求角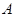 大小;(2)若
大小;(2)若 ,求
,求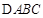 的面积的最大值.
的面积的最大值.