已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(Ⅰ)当a=﹣1时,求函数f(x)的最大值和最小值;
(Ⅱ)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调函数.
已知O为坐标原点,△AOB中,边OA所在的直线方程是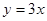 ,边AB所在的直线方程是
,边AB所在的直线方程是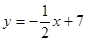 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程。
定义:如果数列 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 为“三角形”数列.对于“三角形”数
为“三角形”数列.对于“三角形”数 列
列 ,如果函数
,如果函数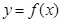 使得
使得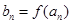 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称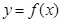 是数列
是数列 的“保三角形函数”,
的“保三角形函数”,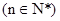 .
.
(Ⅰ)已知 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若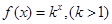 是数列
是数列 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,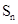 是数列
是数列 的前n项和,且满足
的前n项和,且满足 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数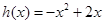 ,
, ,和数列1,
,和数列1,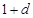 ,
,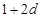 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.
设数列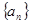 中,若
中,若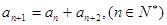 ,则称数列
,则称数列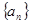 为“凸数列”.
为“凸数列”.
(Ⅰ)设数列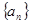 为“凸数列”,若
为“凸数列”,若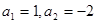 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(Ⅱ)在“凸数列”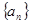 中,求证:
中,求证: ;
;
(Ⅲ)设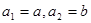 ,若数列
,若数列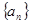 为“凸数列”,求数列前
为“凸数列”,求数列前 项和
项和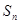 .
.
已知椭圆两个焦点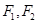 的坐标分别为
的坐标分别为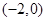 ,
,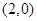 ,并且经过点
,并且经过点 .过左焦点
.过左焦点 ,斜率为
,斜率为 的直线与椭圆交于
的直线与椭圆交于 ,
, 两点.设
两点.设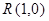 ,延长
,延长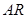 ,
,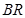 分别与椭圆交于
分别与椭圆交于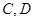 两点.
两点.
(I)求椭圆的标准方程;(II)若点
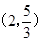 ,求
,求 点的坐标;
点的坐标;
(III)设直线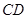 的斜率为
的斜率为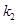 ,求证:
,求证: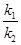 为定值.
为定值.
已知函数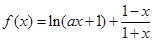 (
(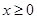 ,
,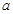 为正实数).
为正实数).
(Ⅰ)若 ,求曲线
,求曲线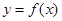 在点
在点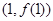 处的切线方程;
处的切线方程;
(Ⅱ)求函数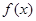 的单调区间;
的单调区间;
(Ⅲ)若函数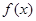 的最小值为
的最小值为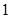 ,求
,求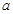 的取值范围.
的取值范围.