选修4-1：几何证明选讲
如图，直线AB为圆的切线，切点为B，点C在圆上，锐角∠ABC的平分线BE交圆于点E，DB垂直BE交圆于D．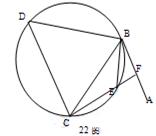
（Ⅰ）证明：DB=DC；
（Ⅱ）设圆的半径为1，BC=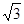
，延长CE交AB于点F，求△BCF外接圆的半径．
袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为
，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．
（1）求袋中原有白球的个数；
（2）求随机变量ξ的概率分布；
（3）求甲取到白球的概率．
设{an}是公比为正数的等比数列，a1＝2，a3＝a2＋4．
（1）求{an}的通项公式；
（2）求数列{an }的前n项和Sn．
六人按下列要求站一横排，分别有多少种不同的站法？
（l）甲不站两端；
（2）甲、乙必须相邻；
（3）甲、乙不相邻；
（4）甲、乙之间间隔两人；
（5）甲不站左端，乙不站右端．
（本小题满分14分）已知数列
的前
项和
，数列
的通项为
，且
满足：
①
；②对任意正整数
都有
成立．
（1）求
与
；
（2）设数列
的前项和为
，求证：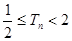
（
）；
（3）数列中是否存在三项，使得这三项按原有的顺序构成等差数列，若存在，求出这三项，若不存在，说明理由．
（本小题满分13分）已知向量
，
，函数
（1）求函数
的最小正周期及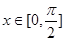
上的最值；
（2）若关于
的方程
在区间
上只有一个实根，求实数
的取值范围．